Engañar sin mentir: relaciones causales en los medios
Las personas con una actitud positiva hacia la ciencia suelen ser más susceptibles, en general, a la influencia de gráficas y la presencia de información cuantitativa. Ello no debería ser motivo de alarma, pero puede producir cierto desasosiego si consideramos que, mucho más frecuentemente de lo que sería deseable, esos elementos son diseñados más para persuadir que para dotar de trasparencia a datos veraces.
En una inmensa mayoría de los casos los datos cuantitativos se utilizan de apoyo para una afirmación sobre la existencia de una relación causa-efecto. De la existencia de esa relación se pueden derivar consecuencias importantes. Veamos algunos ejemplos:
- 12 niños manifiestaron una regresión en su desarrollo después de haber sido vacunados con la vacuna triple vírica.
- El 25% de los muertos en accidentes de tráfico no llevaban puesto el cinturón de seguridad.
- El 95% de las personas que lo han probado están satisfechas con los efectos de «Masbello».
La mayoría de vosotros ya habrá notado la debilidad argumentativa de estas afirmaciones reales. No olvidemos que datos como éstos están en cualquier parte y no siempre estamos alerta cuando nos encontramos con ellos y, lo más importante, nuestra motivación no es un agente neutral en su interpretación.
Maneras de manipular
Simplificando mucho, podemos suponer la existencia de una relación causa-efecto entre A y B, cuando A y B correlacionan, y esa correlación no puede explicarse por la existencia de un tercer factor. Salvo en condiciones de control estricto, el número de factores que pueden explicar esa correlación es desconocido, luego nuestra explicación causal será siempre precaria y provisional, algo que, de partida, debe llevarnos a la precaución.
Una primera forma de intentar pillar al observador desprevenido es magnificar la apariencia de la relación. Lo más habitual es estos casos es dotar a los datos de una apariencia visual que no se corresponde con la información cuantitativa que realmente reflejan. Como muestra un botón:
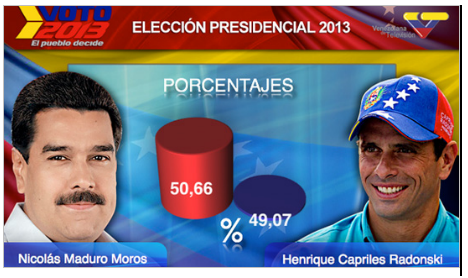
Figura 1. La diferencia de votos entre Maduro y Capriles en las elecciones presidenciales venezolanas de 2013, según una cadena de televisión nacional.
Cierto que este caso no se refiere exactamente a una relación causal (no he podido resistirme a utilizarlo) y que, además de cómico, parece un poco extremo, ¿cierto?. Esta imagen podría valer como compendio de todo lo que se puede hacer mal a la hora de construir una gráfica honesta. En otros casos, sin embargo, las posibilidades de manipulación son más sutiles. Por ejemplo, la mayoría de las personas suele juzgar como más intensa la relación mostrada en la parte derecha de la Figura 2, que la mostrada en la parte izquierda, a pesar de que ambas versiones representan exactamente los mismos datos (Sun, Li y Bonini, 2010).
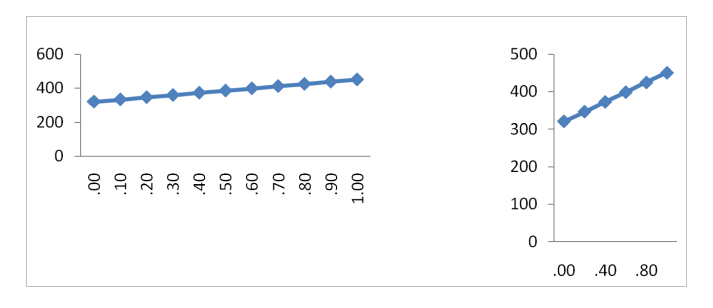
Figura 2. Pendiente visual vs pendiente estadística.
Truncar el eje vertical en un diagrama de barras o resaltar las características visuales de la imagen que favorecen nuestra interpretación favorita son recursos habitualmente utilizados, también en publicaciones científicas. No en vano, uno de los efectos sutiles de una alfabetización estadística eficaz es un cambio en los patrones de movimientos oculares cuando se inspeccionan figuras como las anteriores. Mientras que los individuos menos entrenados miran, fundamentalmente, al interior de la figura, los más habilidosos tienden a realizar desplazamientos entre los ejes y el interior (Woller-Carter et al., 2012).
Por tanto, la primera recomendación de cualquier manual de estilo sería asegurar que las magnitudes perceptivas y las cantidades que éstas representan mantienen una correspondencia intuitiva, y que la figura no oculte información potencialmente importante para falsar la hipótesis del autor. Lo cierto, desafortunadamente, es que las posibilidades de manipulación van más allá de estos trucos, más o menos burdos. La mejor manipulación es aquella en la que se utilizan datos totalmente verídicos y sacan partido de la forma natural e intuitiva que tenemos de responder a la información en el ambiente.
Las formas más habituales de manipulación son aquellas que se aprovechan de nuestra proverbial incapacidad para suspender o demorar un juicio. Ante la necesidad de emitir una opinión, muy raro es el ser humano que se abstiene o se lo piensa antes de hacerlo. O, en otras palabras, ante datos parciales o incompletos, aun siendo totalmente veraces, tendemos a hacer inferencias que, por ende, serán injustificadas. La falta de fundamento de nuestras conclusiones no merma nuestra confianza en las mismas.
Más sorprendentemente, ante datos no sólo veraces, sino incluso completos, la evaluación superficial de los mismos –o la falta de pericia– también puede llevar a juicios inadecuados. Veremos ahora algunos ejemplos sobre nuestra dificultad para analizar información, cuando los datos son pocos y totalmente accesibles.
Los números nos ciegan
Imaginemos que queremos evaluar la relación que existe entre vivir en una gran ciudad a lo largo de 25 años y padecer cáncer, a partir de los siguientes datos recogidos a través de un estudio (hipotético) a gran escala.
Antes de seguir, la incidencia de cáncer según estos datos es exactamente la misma (10%) independientemente del lugar de residencia, aunque el número de casos disponibles para uno de los contextos (30000 personas) es mucho mayor que para el otro (2000 personas).
Esta información puede presentarse de muchas formas distintas. En primer lugar, se puede presentar de forma parcial, bien porque algunas casillas sean desconocidas o bien porque se ocultan intencionadamente. Por ejemplo, no es infrecuente encontrar titulares del tipo en los últimos 25 años hubo 3000 muertes por cáncer en la ciudad X (casilla a). O un 10% de las personas que viven en la ciudad X desarrollan cáncer al cabo de 25 años. Esta última es similar a un 15% de personas con WiFi en casa acaban percibiendo molestias generales de origen inexplicable y “suena” convincente, en parte, porque la adición de información sobre la linealidad del tiempo añade verosimilitud aparente al nexo causal. En todos los casos, sin embargo, falta información que es imprescindible para hacer una aseveración causa-efecto.
Aun presentando toda la información, los juicios que realizamos pueden ser bastante sorprendentes. Por ejemplo, imaginemos que informamos a un grupo de personas de que en la ciudad X, 3000 de 30000 personas desarrollaron cáncer, mientras que en los alrededores fuera de esa ciudad, 200 de 2000 personas desarrollaron cáncer. Incluso en casos como éste, en el que calcular las proporciones relevantes es muy sencillo, un número significativo de personas (entre el 30% y el 70% según la situación experimental concreta; Okan et al., 2012) cae víctima de lo que conoce como inatención al denominador, esto es, la tendencia a comparar sólo los numeradores de los dos cocientes (3000 vs 200) y, por tanto, en este caso, a considerar la ciudad como más peligrosa.
Si los datos, en lugar de presentarse como cocientes, se presentan tal y como aparecen en la Tabla 1, esto es, en forma de frecuencias en la matriz de contingencia, la situación no mejora demasiado. Con los datos presentes en la tabla, una mayoría de los participantes en un experimento inferiría que hay una relación moderadamente positiva entre vivir en una ciudad y contraer cáncer. En términos generales, en las matrices de contingencia los juicios se ven afectados por la probabilidad del efecto (cuanto más frecuente es el efecto, mayores son los juicios, aunque la diferencia entre las dos proporciones se mantenga intacta), y por la probabilidad de la causa (cuanto más frecuente es la causa, más altos son los juicios). Estos dos efectos se han denominado sesgo de densidad del efecto y sesgo de densidad de la causa, respectivamente. El primero es más intenso que el segundo, y de la combinación de ambos resulta que la frecuencia de casos en la casilla a incide mucho más en los juicios que la frecuencia de casos en el resto de casillas (Blanco et al., 2013; Perales y Shanks, 2007).
Interesantemente, el impacto desproporcionado de la casilla a se reduce si no tenemos una hipótesis causal de partida o si la hipótesis es de signo contrario. Tal y como han mostrado Mandel y Vartanian (2009), si el individuo evalúa la información con una hipótesis preventiva (e.g., ¿en qué medida vivir en una gran ciudad previene el cáncer?) incrementa notablemente el peso de las frecuencias de las casillas b y d, y, por tanto, reduce el sesgo de densidad del efecto.
El camino honesto
Los sesgos de densidad y la preponderancia de la casilla a (el número de coincidencias entre causa y efecto) son difíciles de superar. Existen dos factores que juegan a su favor. El primero es la tendencia a atender e incorporar nuestros juicios sólo las características más salientes de los estímulos. En general, son más salientes las magnitudes que las relaciones entre magnitudes (una comparación entre proporciones es, de hecho, una relación entre relaciones, una relación de segundo orden). La otra razón obedece a un mecanismo adaptativo. Solemos buscar causas nuevas para efectos sorprendentes (“¿Por qué me han salido ronchas en la piel? Debe ser algo nuevo que he comido”). En éste, y sólo en este caso, una única coincidencia entre una causa potencial y un efecto suponen una evidencia muy convincente a favor de la existencia de una relación causal entre ambos (para un análisis racional, ver Anderson y Sheu, 1995). Por tanto, en muchas ocasiones naturales, la preponderancia de la casilla a es racional. Es muy posible que, en aquellos casos donde la aplicamos de forma inadecuada, lo que realmente estamos haciendo es utilizar un heurístico (una herramienta mental) que nos ha sido útil en nuestra vida cotidiana.
Si queremos evitar la inatención al denominador, los sesgos de densidad y la preponderancia de la casilla a, la forma más evidente de hacerlo es evitar la información únicamente en formato numérico. Sin embargo, esto no siempre funciona. En un experimento, Perales y Shanks (2008) presentamos a los participantes información entre el uso de un fertilizante y el hecho de un conjunto de plantas floreciese. Para ello, utilizamos iconos representando plantas (cada una de las cuales había sido fertilizada o no, y había florecido o no). En otras palabras, presentamos información como la de la matriz de contigencia, pero de forma individualizada, caso por caso. Si los casos se presentaban uno a uno (tal y como se nos presenta, de hecho, la información en nuestra experiencia cotidiana), o si se presentaban todos los casos juntos, en una sola página, pero intercalados, los participantes mostraban los mismos sesgos que si se presentaba la información en formato numérico. Aparentemente, la información sobre frecuencias naturales es muy evidente al ojo humano y, una vez computadas las frecuencias intuitivas de las cuatro casillas de la matriz de contingencia, se hace el uso habitual de ellas, sin atender a las relaciones entre las mismas.
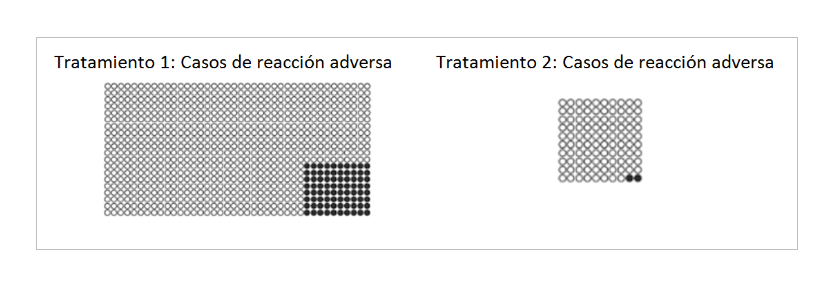
Para que las frecuencias naturales, presentadas de forma icónica, induzcan a un cómputo adecuado de la relación entre causa y efecto se requiere hacer las proporciones y las relaciones entre ellas suficientemente salientes, como en el siguiente ejemplo.
En el estudio de Okan y colaboradores (2012), realizado en el contexto de la comunicación médica, este tipo de presentación prácticamente eliminó la inatención al denominador, pero sólo en aquellas personas con niveles aceptables de alfabetización gráfica. Este resultado coincide con el de Perales y Shanks (2008) en un sentido. Con la presentación segregada (no intercalada) de los casos, el 100% de los participantes pasaron de emitir juicios basados en frecuencias a emitir juicios basados en proporciones, pero sólo algo más de la mitad de los participantes hizo una comparación adecuada entre las dos proporciones relevantes (la otra mitad ignoró la proporción de flores que florecían en ausencia del fertilizante), ello a pesar de que, en nuestro caso, el número plantas fertilizadas y no fertilizadas era el mismo.
Resultados más prometedores han sido publicados por Patricia Cheng y su grupo (ver, por ejemplo, Liljeholm y Cheng, 2009), aunque, desafortunadamente, su estrategia experimental requiere un cierto esfuerzo en diseñar formatos gráficos y formas de inducir una respuesta que son poco viables en los contextos en los que esa información es necesaria. Estos métodos podrían, sin embargo, utilizarse para entrenar a las personas en la interpretación de datos sobre relaciones causales.
Recomendaciones básicas
En resumen, la información cuantitativa sobre relaciones causales puede utilizarse fácilmente para inducir error en los receptores de esa información, y llevar a inducciones erróneas y en muchos casos dañinas. Como trasmisores de esa información, es necesario evitar que nuestras convicciones y nuestro entusiasmo nos lleven a ser nosotros mismos la fuente de distorsión.
- Cuando se utilicen formatos gráficos las magnitudes perceptivas deben seleccionarse de tal manera que su traducción a cantidades sea fiel. A eso se añade que ciertas magnitudes perceptivas son más fáciles de estimar fielmente que otras.
- Elimina fuentes de saliencia innecesarias.
- Evita la información anecdótica, tiene un valor argumentativo desproporcionado a la evidencia que realmente contiene.
- Evita datos en bruto de frecuencias asimétricas (sobrerrepresentación de la causa o el efecto, o de la casilla a de la tabla de contingencia).
- Evita datos numéricos disgregados entre ellos y contrastes entre proporciones con denominadores desiguales.
- Invita a suspender la hipótesis de partida o a interpretar la información presentada bajo la hipótesis contraria a la que pretendes defender.
- Concede a la información sobre tasa base o de grupo de control tanta saliencia perceptiva o atencional como a la tasa de efecto.
- Si utilizas formatos gráficos, haz las relaciones entre las magnitudes relevantes totalmente trasparentes.
- Si puedes, ten en cuenta a quién comunicas. Tanto para la alfabetización gráfica como para la probabilística, existen instrumentos de medida muy breves y suficientemente verificados (García-Retamero y Galesic, 2010).
En las próximas ocasiones que leas la prensa, veas la televisión, oigas las declaraciones de un político (de tu cuerda o no) o leas un prospecto pregúntate, primero, por los intereses de quien aporta los dato; segundo, por la medida en que los datos permitirían contradecirles y, tercero, por la forma en que los datos se han dispuesto. Esos tres sencillos ejercicios mentales deberían ser suficientes para hacerte ver que, en la inmensa mayoría de los casos, los datos más que revelar la verdad, tienden a ocultarla.


En caso de que no hubiese una relación lógica o intuitiva entre flores y fertilizantes, o incluso una relación intuida por el sujeto como opuesta entre ambas variables, se mantiene esta preponderancia de la casilla a? Qué parte de este efecto podría ser un sesgo de confirmación en esta relación?
Esa pregunta, para mí, tiene dos respuestas. Una larga, que daría para otro artículo, y una corta, que es la que pergeño aquí. En todo caso, la pregunta tiene enjundia…
La preponderancia de la casilla a probablemente tiene varios orígenes, pero no es necesario que ya tengas previamente la creencia de que X e Y están causalmente relacionados (aunque lógicamente, si vienes con esa creencia, necesitarás más evidencia en el sentido opuesto para cambiarla; las creencias previas pueden llegar incluso a bloquear todo aprendizaje posterior).
Tampoco puede hablarse de un sesgo confirmatorio en el sentido estricto, porque si tu crees que hay una relación y buscas confirmarla, no sólo se incrementaría el peso de la casilla a, sino también el de la casilla d (y sin embargo d es la casilla que menos peso tiene, en casi todos los casos).
Lo que parece importante es la hipótesis de partida («positive test bias»), hasta el punto de que, simplemente cambiando la redacción de la pregunta (de generativa a preventiva), con las mismas creencias previas y la misma evidencia estadística disponible, la mayor preponderancia pasa a la casilla b (échale un vistazo al artículo de Mandel y Vartarnian que se cita en el post).
Lo que parece cambiar de un caso a otro es el evento a explicar. En una hipótesis generativa, el evento a explicar(subjetivamente) es la aparición del efecto, mientras que en la preventiva es la no-aparición del efecto. En otras palabras, tratas la no aparición como un hecho en sí (y diriges tu atención hacia ella). Esa misma idea ya estaba en un artículo algo antiguo de Linda Van Hamme y Ed Wasserman. Aprendemos más sobre la ausencia de algo cuando esa ausencia es significativa.
De todas formas, la preponderancia de la casilla a bajo hipótesis generativas es algo más intensa que la preponderancia de la casilla b bajo hipótesis preventiva. Eso parece deberse a que nuestro sistema trabaja mejor con la información positiva que con la negativa («positive event bias»).